- Ebisu: intelligent quiz scheduling
Consider a student memorizing a set of facts.
- Which facts need reviewing?
- How does the student’s performance on a review change the fact’s future review schedule?
Ebisu is a public-domain library that answers these two questions. It is intended to be used by software developers writing quiz apps, and provides a simple API to deal with these two aspects of scheduling quizzes:
predictRecallgives the current recall probability for a given fact.updateRecalladjusts the belief about future recall probability given a quiz result.
Behind these two simple functions, Ebisu is using a simple yet powerful model of forgetting, a model that is founded on Bayesian statistics and exponential forgetting.
With this system, quiz applications can move away from “daily review piles” caused by less flexible scheduling algorithms. For instance, a student might have only five minutes to study today; an app using Ebisu can ensure that only the facts most in danger of being forgotten are reviewed.
Ebisu also enables apps to provide an infinite stream of quizzes for students who are cramming. Thus, Ebisu intelligently handles over-reviewing as well as under-reviewing.
This document is a literate source: it contains a detailed mathematical description of the underlying algorithm as well as source code for a Python implementation (requires Scipy and Numpy). Separate implementations in other languages are detailed below.
The next section is a Quickstart guide to setup and usage. See this if you know you want to use Ebisu in your app.
Then in the How It Works section, I contrast Ebisu to other scheduling algorithms and describe, non-technically, why you should use it.
Then there’s a long Math section that details Ebisu’s algorithm mathematically. If you like Beta-distributed random variables, conjugate priors, and marginalization, this is for you. You’ll also find the key formulas that implement predictRecall and updateRecall here.
Nerdy details in a nutshell: Ebisu begins by positing a Beta prior on recall probability at a certain time. As time passes, the recall probability decays exponentially, and Ebisu handles that nonlinearity exactly and analytically—it requires only a few Beta function evaluations to predict the current recall probability. Next, a quiz is modeled as a binomial trial whose underlying probability prior is this non-conjugate nonlinearly-transformed Beta. Ebisu approximates the non-standard posterior with a new Beta distribution by matching its mean and variance, which are also analytically tractable, and require a few evaluations of the Beta function.
Finally, the Source Code section presents the literate source of the library, including several tests to validate the math.
Install pip install ebisu (both Python3 and Python2 ok 🤠).
Data model For each fact in your quiz app, you store a model representing a prior distribution. This is a 3-tuple: (alpha, beta, t) and you can create a default model for all newly learned facts with ebisu.defaultModel. (As detailed in the Choice of initial model parameters section, alpha and beta define a Beta distribution on this fact’s recall probability t time units after it’s most recent review.)
Predict a fact’s current recall probability ebisu.predictRecall(prior: tuple, tnow: float) -> float where prior is this fact’s model and tnow is the current time elapsed since this fact’s most recent review. tnow may be any unit of time, as long as it is consistent with the half life’s unit of time. The value returned by predictRecall is a probability between 0 and 1.
Update a fact’s model with quiz results ebisu.updateRecall(prior: tuple, success: int, total: int, tnow: float) -> tuple where prior and tnow are as above, and where success is the number of times the student successfully exercised this memory during the current review session out of total times—this way your quiz app can review the same fact multiple times in one sitting. Bonus: you can also pass in a floating point success between 0 and 1 for soft-binary quizzes! The returned value is this fact’s new prior model—the old one can be discarded.
IPython Notebook crash course For a conversational introduction to the API in the context of a mocked quiz app, see this IPython Notebook crash course.
Further information Module docstrings in a pinch but full details plus literate source below, under Source code.
Alternative implementations Ebisu.js is a JavaScript port for browser and Node.js. ebisu-java is for Java and JVM languages. ebisu_dart is a Dart port for browser and native targets. obliviate is available for .NET.
There are many scheduling schemes, e.g.,
- Anki, an open-source Python flashcard app (and a closed-source mobile app),
- the SuperMemo family of algorithms (Anki’s is a derivative of SM-2),
- Memrise.com, a closed-source webapp,
- Duolingo has published a blog entry and a conference paper/code repo on their half-life regression technique,
- the Leitner and Pimsleur spacing schemes (also discussed in some length in Duolingo’s paper).
- Also worth noting is Michael Mozer’s team’s Bayesian multiscale models, e.g., Mozer, Pashler, Cepeda, Lindsey, and Vul’s 2009 NIPS paper and subsequent work.
Many of these are inspired by Hermann Ebbinghaus’ discovery of the exponential forgetting curve, published in 1885, when he was thirty-five. He memorized random consonant–vowel–consonant trigrams (‘PED’, e.g.) and found, among other things, that his recall decayed exponentially with some time-constant.
Anki and SuperMemo use carefully-tuned mechanical rules to schedule a fact’s future review immediately after its current review. The rules can get complicated—I wrote a little field guide to Anki’s, with links to the source code—since they are optimized to minimize daily review time while maximizing retention. However, because each fact has simply a date of next review, these algorithms do not gracefully accommodate over- or under-reviewing. Even when used as prescribed, they can schedule many facts for review on one day but few on others. (I must note that all three of these issues—over-reviewing (cramming), under-reviewing, and lumpy reviews—have well-supported solutions in Anki by tweaking the rules and third-party plugins.)
Duolingo’s half-life regression explicitly models the probability of you recalling a fact as \(2^{-Δ/h}\), where Δ is the time since your last review and \(h\) is a half-life. In this model, your chances of passing a quiz after \(h\) days is 50%, which drops to 25% after \(2 h\) days. They estimate this half-life by combining your past performance and fact metadata in a large-scale machine learning technique called half-life regression (a variant of logistic regression or beta regression, more tuned to this forgetting curve). With each fact associated with a half-life, they can predict the likelihood of forgetting a fact if a quiz was given right now. The results of that quiz (for whichever fact was chosen to review) are used to update that fact’s half-life by re-running the machine learning process with the results from the latest quizzes.
The Mozer group’s algorithms also fit a hierarchical Bayesian model that links quiz performance to memory, taking into account inter-fact and inter-student variability, but the training step is again computationally-intensive.
Like Duolingo and Mozer’s approaches, Ebisu explicitly tracks the exponential forgetting curve to provide a list of facts sorted by most to least likely to be forgotten. However, Ebisu formulates the problem very differently—while memory is understood to decay exponentially, Ebisu posits a probability distribution on the half-life and uses quiz results to update its beliefs in a fully Bayesian way. These updates, while a bit more computationally-burdensome than Anki’s scheduler, are much lighter-weight than Duolingo’s industrial-strength approach.
This gives small quiz apps the same intelligent scheduling as Duolingo’s approach—real-time recall probabilities for any fact—but with immediate incorporation of quiz results, even on mobile apps.
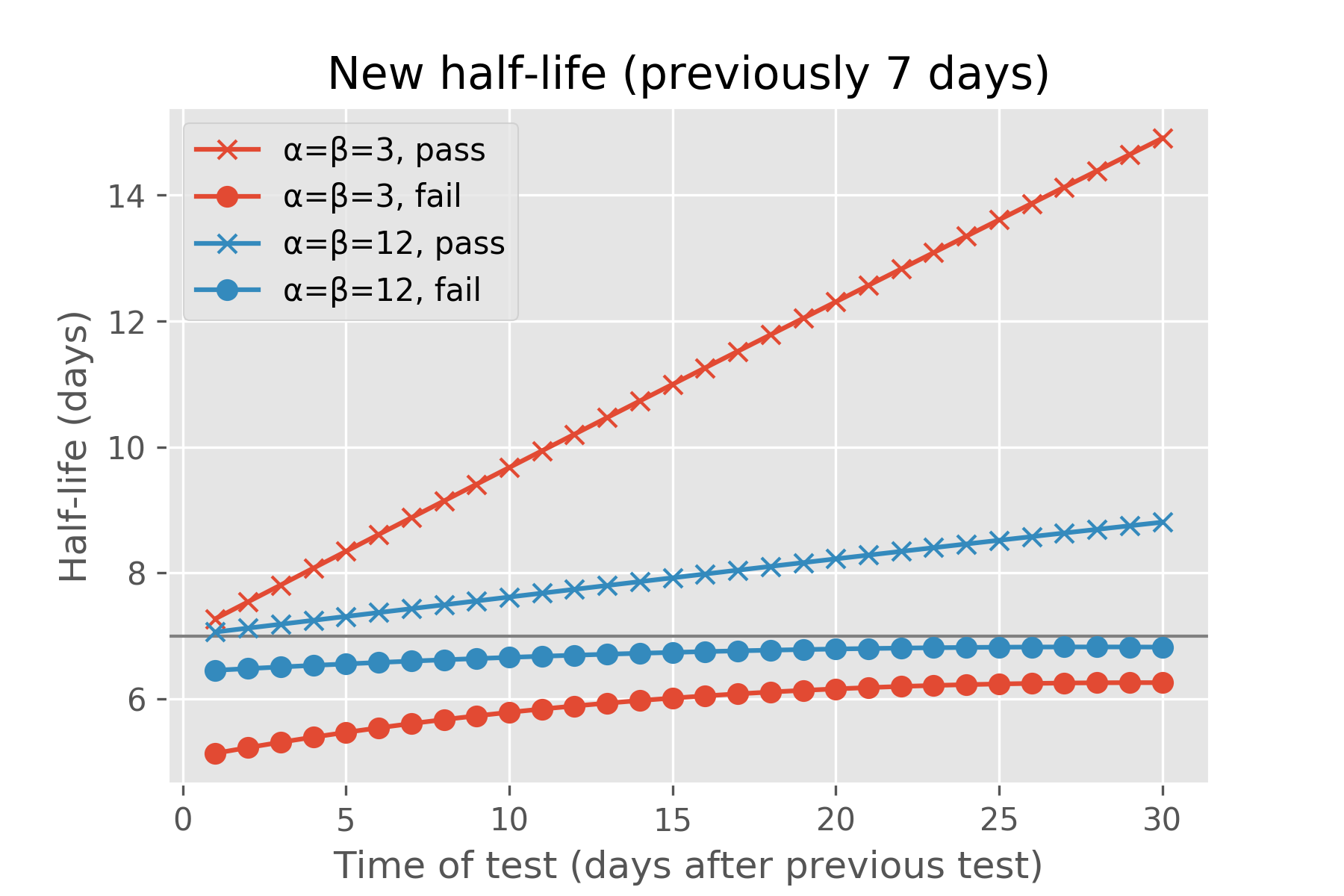
To appreciate this further, consider this example. Imagine a fact with half-life of a week: after a week we expect the recall probability to drop to 50%. However, Ebisu can entertain an infinite range of beliefs about this recall probability: it can be very uncertain that it’ll be 50% (the “α=β=3” model below), or it can be very confident in that prediction (“α=β=12” case):
Under either of these models of recall probability, we can ask Ebisu what the expected half-life is after the student is quizzed on this fact a day, a week, or a month after their last review, and whether they passed or failed the quiz:
If the student correctly answers the quiz, Ebisu expects the new half-life to be greater than a week. If the student answers correctly after just a day, the half-life rises a little bit, since we expected the student to remember this fact that soon after reviewing it. If the student surprises us by failing the quiz just a day after they last reviewed it, the projected half-life drops. The more tentative “α=β=3” model aggressively adjusts the half-life, while the more assured “α=β=12” model is more conservative in its update. (Each fact has an α and β associated with it and I explain what they mean mathematically in the next section. Also, the code for these two charts is below.)
Similarly, if the student fails the quiz after a whole month of not reviewing it, this isn’t a surprise—the half-life drops a bit from the initial half-life of a week. If she does surprise us, passing the quiz after a month of not studying it, then Ebisu boosts its expected half-life—by a lot for the “α=β=3” model, less for the “α=β=12” one.
Currently, Ebisu treats each fact as independent, very much like Ebbinghaus’ nonsense syllables: it does not understand how facts are related the way Duolingo can with its sentences. However, Ebisu can be used in combination with other techniques to accommodate extra information about relationships between facts.
Let’s begin with a quiz. One way or another, we’ve picked a fact to quiz the student on, \(t\) days (the units are arbitrary since \(t\) can be any positive real number) after her last quiz on it, or since she learned it for the first time.
We’ll model the results of the quiz as a Bernoulli experiment—we’ll later expand this to a binomial experiment. So for Bernoulli quizzes, \(x_t ∼ Bernoulli(p)\); \(x_t\) can be either 1 (success) with probability \(p_t\), or 0 (fail) with probability \(1-p_t\). Let’s think about \(p_t\) as the recall probability at time \(t\)—then \(x_t\) is a coin flip, with a \(p_t\)-weighted coin.
The Beta distribution happens to be the conjugate prior for the Bernoulli distribution. So if our a priori belief about \(p_t\) follow a Beta distribution, that is, if \[p_t ∼ Beta(α_t, β_t)\] for specific \(α_t\) and \(β_t\), then observing the quiz result updates our belief about the recall probability to be: \[p_t | x_t ∼ Beta(α_t + x_t, β_t + 1 - x_t).\]
Aside 0 If you see a gibberish above instead of a mathematical equation (it can be hard to tell the difference sometimes…), you’re probably reading this on GitHub instead of the main Ebisu website which has typeset all equations with MathJax. Read this document there.
Aside 1 Notice that since \(x_t\) is either 1 or 0, the updated parameters \((α + x_t, β + 1 - x_t)\) are \((α + 1, β)\) when the student correctly answered the quiz, and \((α, β + 1)\) when she answered incorrectly.
Aside 2 Even if you’re familiar with Bayesian statistics, if you’ve never worked with priors on probabilities, the meta-ness here might confuse you. What the above means is that, before we flipped our \(p_t\)-weighted coin (before we administered the quiz), we had a specific probability distribution representing the coin’s weighting \(p_t\), not just a scalar number. After we observed the result of the coin flip, we updated our belief about the coin’s weighting—it still makes total sense to talk about the probability of something happening after it happens. Said another way, since we’re being Bayesian, something actually happening doesn’t preclude us from maintaining beliefs about what could have happened.
This is totally ordinary, bread-and-butter Bayesian statistics. However, the major complication arises when the experiment took place not at time \(t\) but \(t_2\): we had a Beta prior on \(p_t\) (probability of recall at time \(t\)) but the test is administered at some other time \(t_2\).
How can we update our beliefs about the recall probability at time \(t\) to another time \(t_2\), either earlier or later than \(t\)?
Our old friend Ebbinghaus comes to our rescue. According to the exponentially-decaying forgetting curve, the probability of recall at time \(t\) is \[p_t = 2^{-t/h},\] for some notional half-life \(h\). Let \(t_2 = δ·t\). Then, \[p_{t_2} = p_{δ t} = 2^{-δt/h} = (2^{-t/h})^δ = (p_t)^δ.\] That is, to fast-forward or rewind \(p_t\) to time \(t_2\), we raise it to the \(δ = t_2 / t\) power.
Unfortunately, a Beta-distributed \(p_t\) becomes non-Beta-distributed when raised to any positive power \(δ\). For a quiz with recall probability given by \(p_t ∼ Beta(12, 12)\) for \(t\) one week after the last review (the middle histogram below), \(δ > 1\) shifts the density to the left (lower recall probability) while \(δ < 1\) does the opposite. Below shows the histogram of recall probability at the original half-life of seven days compared to that after two days (\(δ = 0.3\)) and three weeks (\(δ = 3\)).

We could approximate this \(δ\) with a Beta random variable, but especially when over- or under-reviewing, the closest Beta fit is very poor. So let’s derive analytically the probability density function (PDF) for \(p_t^δ\). Recall the conventional way to obtain the density of a nonlinearly-transformed random variable. Since the new random variable \[p_{t_2} = g(p_t) = (p_t)^δ,\] and the inverse of this transformation is \[p_t = g^{-1}(p_{t_2}) = (p_{t_2})^{1/δ},\] the transformed (exponentiated) random variable has probability density \begin{align} P(p_{t_2}) &= P\left(g^{-1}(p_{t_2})\right) ⋅ \frac{∂}{∂p_{t_2}} g^{-1}(p_{t_2}) \\ &= Beta(p_{t_2}^{1/δ}; α, β) ⋅ \frac{p_{t_2}^{1/δ - 1}}{δ}, \end{align} since \(P(p_t) = Beta(p_t; α, β)\), the Beta density on the recall probability at time \(t\), and \(\frac{∂}{∂p_{t_2}} g^{-1}(p_{t_2})^{1/δ} = \frac{p_{t_2}^{1/δ - 1}}{δ}\). Following some algebra, the final density is \[ P(p; p_t^δ) = \frac{p^{α/δ - 1} · (1-p^{1/δ})^{β-1}}{δ · B(α, β)}, \] where \(B(α, β) = Γ(α) · Γ(β) / Γ(α + β)\) is beta function (also the normalizing denominator in the Beta density—confusing, sorry), and \(Γ(·)\) is the gamma function, a generalization of factorial. Throughout this document, I use \(P(x; X)\) to denote the density of the random variable \(X\) as a function of the algebraic variable \(x\).
Robert Kern noticed that this is a generalized Beta of the first kind, or GB1, random variable: \[p_t^δ ∼ GB1(p; 1/δ, 1, α; β)\] When \(δ=1\), that is, at exactly the half-life, recall probability is simply the initial Beta we started with.
We will use the density of \(p_t^δ\) to reach our two most important goals:
- what’s the recall probability of a given fact right now?, and
- how do I update my estimate of that recall probability given quiz results?
To check the above derivation in Wolfram Alpha, type in
p^((a-1)/d) * (1 - p^(1/d))^(b-1) / Beta[a,b] * D[p^(1/d), y].To check it in Sympy, copy-paste the following into the Sympy Live Shell (or save it in a file and run):
from sympy import symbols, simplify, diff p_1, p_2, a, b, d, den = symbols('p_1 p_2 α β δ den', positive=True, real=True) prior_t = p_1**(a - 1) * (1 - p_1)**(b - 1) / den prior_t2 = simplify(prior_t.subs(p_1, p_2**(1 / d)) * diff(p_2**(1 / d), p_2)) prior_t2 # or print(prior_t2)which produces
p_2**((α - δ)/δ)*(1 - p_2**(1/δ))**(β - 1)/(den*δ).And finally, we can use Monte Carlo to generate random draws from \(p_t^δ\), for specific α, β, and δ, and comparing sample moments against the GB1's analytical moments per Wikipedia, \(E\left[(p_{t}^{δ})^N\right]=\frac{B(α + δ N, β)}{B(α, β)}\):
(α, β, δ) = 5, 4, 3 import numpy as np from scipy.stats import beta as betarv from scipy.special import beta as betafn prior_t = betarv.rvs(α, β, size=100_000) prior_t2 = prior_t**δ Ns = np.array([1, 2, 3, 4, 5]) sampleMoments = [np.mean(prior_t2**N) for N in Ns] analyticalMoments = betafn(α + δ * Ns, β) / betafn(α, β) print(list(zip(sampleMoments, analyticalMoments)))which produces this tidy table of the first five non-central moments:
analytical sample % difference 0.2121 0.2122 0.042% 0.06993 0.06991 -0.02955% 0.02941 0.02937 -0.1427% 0.01445 0.01442 -0.2167% 0.007905 0.007889 -0.2082% We check both mathematical derivations and their programmatic implementations by comparing them against Monte Carlo as part of an extensive unit test suite in the code below.
Let’s see how to get the recall probability right now. Recall that we started out with a prior on the recall probabilities \(t\) days after the last review, \(p_t ∼ Beta(α, β)\). Letting \(δ = t_{now} / t\), where \(t_{now}\) is the time currently elapsed since the last review, we saw above that \(p_t^δ\) is GB1-distributed. Wikipedia kindly gives us an expression for the expected recall probability right now, in terms of the Beta function, which we may as well simplify to Gamma function evaluations: \[ E[p_t^δ] = \frac{B(α+δ, β)}{B(α,β)} = \frac{Γ(α + β)}{Γ(α)} · \frac{Γ(α + δ)}{Γ(α + β + δ)} \]
A quiz app can calculate the average current recall probability for each fact using this formula, and thus find the fact most at risk of being forgotten.
Mentioning a quiz app reminds me—you may be wondering how to pick the prior triple \([α, β, t]\) initially, for example when the student has first learned a fact.
Set \(t\) equal to your best guess of the fact’s half-life. In Memrise, the first quiz occurs four hours after first learning a fact; in Anki, it’s a day after. To mimic these, set \(t\) to four hours or a day, respectively. In my apps, I set initial \(t\) to a quarter-hour (fifteen minutes).
Then, pick \(α = β > 1\). First, for \(t\) to be a half-life, \(α = β\). Second, a higher value for \(α = β\) means higher confidence that the true half-life is indeed \(t\), which in turn makes the model less sensitive to quiz results—this is, after all, a Bayesian prior. A good default is \(α = β = 3\), which lets the algorithm aggressively change the half-life in response to quiz results.
Quiz apps that allow a students to indicate initial familiarity (or lack thereof) with a flashcard should modify the initial half-life \(t\). It remains an open question whether quiz apps should vary initial \(α = β\) for different flashcards.
Now, let us turn to the final piece of the math, how to update our prior on a fact’s recall probability when a quiz result arrives.
Recall that our quiz app might ask the student to exercise the same memory, one or more times in one sitting (perhaps conjugating the same verb in two different sentences). Therefore, the student’s recall of that memory is a binomial experiment, which is parameterized by \(k\) successes out of \(n\) attempts, with \(0 ≤ k ≤ n\) and \(n ≥ 1\). For many quiz applications, \(n = 1\), so this simplifies to a Bernoulli experiment.
Nota bene. The \(n\) individual sub-trials that make up a single binomial experiment are assumed to be independent of each other. If your quiz application tells the user that, for example, they incorrectly conjugated a verb, and then later in the same review session, asks the user to conjugate the verb again (perhaps in the context of a different sentence), then the two sub-trials are likely not independent, unless the user forgot that they were just asked about that verb. Please get in touch if you want feedback on whether your quiz app design might be running afoul of this caveat.
Let us assume that the quiz happens at \(t_2\) time units after last recall. We had a prior on the recall probability at this \(t_2 = δ t\). Now, given a quiz at \(t_2\) that yielded \(k\) and \(n\), what is the posterior on the recall probability? (I will drop all subscripts for the time being but do note that the recall probability \(p\), and the quiz results \(k\), are indexed by time and should be \(p_{t_2}\) and \(k_{t_2}\).)
One option could be this: since we have analytical expressions for the mean and variance of the prior on the recall probability’s prior—\(p_t^δ\) follows the GB1 density—convert these to the closest Beta distribution and straightforwardly update with the Bernoulli or binomial likelihoods as mentioned above. However, we can do much better.
By application of Bayes rule, the posterior is \[Posterior(p|k, n) = \frac{Prior(p) · Lik(k|p,n)}{\int_0^1 Prior(p) · Lik(k|p,n) \, dp}.\] Here, “prior” refers to the GB1 density \(P(p_t^δ)\) derived above. \(Lik\) is the binomial likelihood: \(Lik(k|p,n) = \binom{n}{k} p^k (1-p)^{n-k}\). The denominator is the marginal probability of the observation \(k\). (In the above, all recall probabilities \(p\) and quiz results \(k\) are at the same \(t_2 = t · δ\), but we’ll add time subscripts again below.)
Combining all these into one expression, we have: \[ Posterior(p|k, n) = \frac{ p^{α/δ - 1} (1-p^{1/δ})^{β - 1} p^k (1-p)^{n-k} }{ \int_0^1 p^{α/δ - 1} (1-p^{1/δ})^{β - 1} p^k (1-p)^{n-k} \, dp }, \] where note that the big integrand in the denominator is just the numerator.
We use two helpful facts now. The more important one is that \[ \int_0^1 p^{α/δ - 1} (1-p^{1/δ})^{β - 1} \, dp = δ ⋅ B(α, β), \] when \(α, β, δ > 0\). We’ll use this fact several times in what follows—you can see the form of this integrand in the big integrand in the above posterior.
The second helpful fact gets us around that pesky \((1-p)^{n-k}\). By applying the binomial theorem, we can see that \[ \int_0^1 f(x) (1-x)^n \, dx = \sum_{i=0}^{n} \left[ \binom{n}{i} (-1)^i \int_0^1 x^i f(x) \, dx \right], \] for integer \(n > 0\).
Putting these two facts to use, we can show that the posterior at time \(t_2\) is \[ Posterior(p; p_{t_2}|k, n) = \frac{ \sum_{i=0}^{n-k} \binom{n-k}{i} (-1)^i p^{α / δ + k + i - 1} (1-p^{1/δ})^{β - 1} }{ δ \sum_{i=0}^{n-k} \binom{n-k}{i} (-1)^i ⋅ B(α + δ (k + i), \, β) }. \]
We’ve added back the time subscripts to emphasize that this is the posterior on recall probability at time \(t_2\), the time of the quiz (though for lightness I left the subscript off \(k_{t_2}\) and \(n_{t_2}\)). I’d like to have a posterior at any arbitrary time \(t'\), just in case \(t_2\) happens to be very small or very large. It turns out this posterior can be analytically time-transformed just like we did in the Moving Beta distributions through time section above, except instead of moving a Beta through time, we move this analytic posterior. Just as we have \(δ=t_2/t\) to go from \(t\) to \(t_2\), let \(ε=t' / t_2\) to go from \(t_2\) to \(t'\).
Then, as described above and following the rules for nonlinear transforms of random variables: \begin{align} P(p; p_{t'} | k_{t_2}, n_{t_2}) &= Posterior \left(p^{1/ε}; p_{t_2}|k_{t_2}, n_{t_2} \right) ⋅ \frac{1}{ε} p^{1/ε - 1} \\ &= \frac{ \sum_{i=0}^{n-k} \binom{n-k}{i} (-1)^i p^{\frac{α + δ (k + i)}{δ ε} - 1} (1-p^{1/(δε)})^{β - 1} }{ δε \sum_{i=0}^{n-k} \binom{n-k}{i} (-1)^i ⋅ B(α + δ (k + i), \, β) }. \end{align} The denominator is the same in this \(t'\)-time-shifted posterior since it’s just a normalizing constant (and not a function of probability \(p\)) but the numerator retains the same shape as the original, allowing us to use one of our helpful facts above to derive this transformed posterior’s moments. The \(N\)th moment, \(E[p_{t'}^N] \), is: \[ m_N = \frac{ \sum_{i=0}^{n-k} \binom{n-k}{i} (-1)^i ⋅ B(α + (i+k)δ + N δ ε, \, β) }{ \sum_{i=0}^{n-k} \binom{n-k}{i} (-1)^i ⋅ B(α + (i+k)δ, \, β) }. \] With these moments of our final posterior at arbitrary time \(t'\) in hand, we can moment-match to recover a Beta-distributed random variable that serves as the new prior. Recall that a distribution with mean \(μ\) and variance \(σ^2\) can be fit to a Beta distribution with parameters:
- \(\hat α = (μ(1-μ)/σ^2 - 1) ⋅ μ\) and
- \(\hat β = (μ(1-μ)/σ^2 - 1) ⋅ (1-μ)\).
In the simple \(n=1\) case of Bernoulli quizzes, these moments simplify further (though in my experience, the code is simpler for the general binominal case).
To summarize the update step: you started with a flashcard whose memory model was \([α, β, t]\). That is, the prior on recall probability after \(t\) time units since the previous encounter is \(Beta(α, β)\). At time \(t_2\), you administer a quiz session that results in \(k\) successful recollections of this flashcard, out of a total of \(n\).
- The updated model is
- \([μ (μ(1-μ)/σ^2 - 1), \, (1-μ) (μ(1-μ)/σ^2 - 1), \, t']\) for any arbitrary time \(t'\), and for
- \(δ = t_2/t\),
- \(ε=t'/t_2\), where both
- \(μ = m_1\) and
- \(σ^2 = m_2 - μ^2\) come from evaluating the appropriate \(m_N\):
- \( m_N = \frac{ \sum_{i=0}^{n-k} \binom{n-k}{i} (-1)^i ⋅ B(α + (i+k)δ + N δ ε, \, β) }{ \sum_{i=0}^{n-k} \binom{n-k}{i} (-1)^i ⋅ B(α + (i+k)δ, \, β) } \).
- \([μ (μ(1-μ)/σ^2 - 1), \, (1-μ) (μ(1-μ)/σ^2 - 1), \, t']\) for any arbitrary time \(t'\), and for
Note The Beta function \(B(a,b)=Γ(a) Γ(b) / \Gamma(a+b)\), being a function of a rapidly-growing function like the Gamma function (it is a generalization of factorial), may lose precision in the above expressions for unusual α and β and δ and ε. Addition and subtraction are risky when dealing with floating point numbers that have lost much of their precision. Ebisu takes care to use log-Beta and
logsumexpto minimize loss of precision.
For this section, let’s restrict ourselves to \(n=1\); a review consists of just one quiz. But imagine if, instead of a Bernoulli trial that yields a binary 0 or 1, you had a “soft-binary” or “fuzzy” quiz result. Could we adjust the Ebisu model to consume such non-binary quiz results? As luck would have it, Stack Exchange user @mef has invented a lovely way to model this.
Let \(x \sim Bernoulli(p)\) be the true Bernoulli draw, that is, the binary quiz result if there was no ambiguity or fuzziness around the student’s performance: \(x\) is either 0 or 1. However, rather than observe \(x\), we actually observe a “noisy report” \((z | x) \sim Bernoulli(q_x)\) where
- \(q_1 = P(z = 1 | x = 1)\) while
- \(q_0 = P(z = 1 | x = 0)\).
Note that, in the true-binary case, without fuzziness, \(q_1 = 1\) and \(q_0 = 0\), but in the soft-binary case, these two parameters are independent and free for you to specify as any numbers between 0 and 1 inclusive.
Let’s work through the analysis, and then we’ll consider the question of how a real quiz app might set these parameters.
The posterior at time \(t_2\), i.e., at the time of the quiz, \[ P(p; p_{t_2} | z_{t_2}) = \frac{Prior(p) \cdot Lik(z | p)}{\int_0^1 Prior(p) \cdot Lik(z|p) dp} \] follows along similar lines as above in the binomial case—the prior is the GB1 prior on the recall probability at time \(t_2\), and the denominator above is just the definite integral of the numerator—except with a different likelihood. To describe that likelihood, we can take advantage of @mef’s derivation that the joint probability \(P(p, x, z) = P(z|x) P(x|p) P(p)\), then marginalize out \(x\) and divide by the marginal on \(p\). So, first, marginalize: \[ P(p, z) = \sum_{x=0}^1 P(p, x, z) = P(p) \sum_{x=0}^1 P(z|x) P(x|p), \] and then divide: \[ \frac{P(p, z)}{P(p)} = Lik(z | p) = \sum_{x=0}^1 P(z|x) P(x|p) \] to get the likelihood. You could have written down last statement, \(Lik(z | p) = \sum_{x=0}^1 P(z|x) P(x|p)\), since it follows from definitions but the above long-winded way was how I first saw it, via @mef’s expression for the joint probability. (In the above paragraph, I’ve dropped the \(t_2\) subscript, and continue to drop it until we need to talk about recall probabilities at other times.)
Let’s break this likelihood into its two cases: first, for observed failed quizzes, \begin{align} Lik(z=0 | p) &= P(z=0|x=0) P(x=0|p) + P(z=0|x=1) P(x=1|p) \\ &= (1-q_0)(1-p) + (1-q_1) p. \end{align} And following the same pattern, for observed successful quizzes: \begin{align} Lik(z=1| p) &= P(z=1|x=0) P(x=0|p) + P(z=1|x=1) P(x=1|p) \\ &=q_0 (1-p) + q_1 p. \end{align}
Recall that, while the above posterior is on the recall at the time of the quiz \(t_2\), we want the flexibility to time-travel it to any time \(t' = ε ⋅ t_2\). We’ve done this twice already—first to transform the Beta prior on recall after \(t\) to \(t_2 = δ ⋅ t\), and then again to transform the binomial posterior from the quiz time \(t_2\) to any \(t' = ε ⋅ t_2\). Let’s do it a third time. The pattern is the same as before: \[ P(p; p_{t'}|z_{t_2}) ∝ Prior(p^{1/ε}) ⋅ Lik(p^{1/ε}) ⋅ \frac{1}{ε} p^{1/ε - 1} \] where the \(∝\) symbol is read “proportional to” and just means that the expression on the right has to be normalized (divide it by its integral) to ensure the result is a true probability density whose definite integral sums to one.
We can represent the likelihood of any \(n=1\) quiz—binary and noisy!—as \(Lik(z|p) = r p + s\) for some \(r\) and \(s\). Then, \[ P(p; p_{t'}|z_{t_2}) = \frac{ \left( r p^{\frac{α + δ}{δ ε} - 1} + s p^{\frac{α}{δ ε}-1} \right) \left( 1-p^{\frac{1}{δ ε}} \right)^{β - 1} }{ δ ε (r B(α + δ, β) + s B(α, β)) }. \] The normalizing denominator comes from \(\int_0^1 p^{a/x - 1} (1-p^{1/x})^{b - 1} dp = x ⋅ B(a, b)\), which we also used in the binomial case above. This fact is also very helpful to evaluate the moments of this posterior: \[ m_N = E\left[ p_{t'}^N\right] = \frac{ c B(α + δ(1 + N ε), β) + s B(α + δ N ε, β) }{ r B(α + δ, β) + s B(α, β) }. \] Note that this relies on \(n=1\) quizzes, with a single review per fact.
- For \(z=0\), i.e., a failed quiz,
- \(r = q_0 - q_1\) (-1 for a binary non-fuzzy quiz)
- \(s = 1-q_0\) (1 for a binary non-fuzzy quiz).
- For \(z=1\), a successful quiz,
- \(r = q_1 - q_0\) (1 for a binary non-fuzzy quiz)
- \(s = q_0\) (0 for a binary non-fuzzy quiz).
Sharp-eyed readers will notice that, for the successful binary quiz and \(δ ε = 1\), i.e., when \(t' = t\) and the posterior is moved from the recall at the quiz time back to the time of the initial prior, this posterior is simply a Beta density. We’ll revisit this observation in the appendix.
It’s comforting that these moments for the non-fuzzy binary case agree with those derived for the general \(n\) case in the previous section—in the no-noise case, \(q_x = x\).
With these expressions, the first and second (non-central) moments of the posterior can be evaluated for a given \(z\). The two moments can then be moment-matched to the nearest Beta distribution to yield an updated model—the details of those final steps are the same as the binomial case discussed in the previous section.
Let’s consider how a flashcard app might use this statistical machinery for soft-binary quizzes, where the quiz result is a decimal value between 0 and 1, inclusive. A very reasonable convention would be to treat values greater 0.5 as \(z=1\) and the rest as \(z=0\). But this still leaves open two independent parameters, \(q_1 = p(z = 1 | x = 1)\) and \(q_0 = p(z = 1 | x = 0)\). These paramters can be seen as,
- what are the odds that the student really knew the answer but it just slipped her mind, because of factors other than her memory—what she ate just before the quiz, how much coffee she’s had, her stress level, the ambient noise? This is \(q_1\).
- And similarly, suppose the student really had forgotten the answer: what are the odds that she got the quiz right? This is \(q_0\), and can capture situations like multiple-choice quizzes, or cases where the “successful recall” was actually due to a chance event other than memory recall (perhaps the student saw the answer on the news). Or, consider how often you’ve remembered the answer after considerable struggle but were sure that had circumstances been slightly different, you’d have failed the quiz?
One appealing way to set both these parameters for a given fuzzy quiz result is, given a 0 <= result <= 1,
- set \(q_1 = \max(result, 1-result)\), and then
- \(q_0 = 1-q_1\).
- Let \(z = result > 0.5\).
This algorithm is appealing because the posterior models have halflife that smoothly vary between the hard-fail and the full-pass case. That is, if a quiz’s Ebisu model had a halflife of 10 time units, and a hard Bernoulli fail would drop the halflife to 8.5 and a full Bernoulli pass would raise it to 15, fuzzy results between 0 and 1 would yield updated models with halflife smoothly varying between 8.5 and 15, with a fuzzy result of 0.5 yielding a halflife of 10. This is sensible because \(q_0 = q_1 = 0.5\) implies your fuzzy quiz result is completely uninformative about your actual memory, so Ebisu has no choice but to leave the model alone.
Another kind of feedback that users can provide is indication that a quiz was either too late or too early, or in other words, the user wants to see a flashcard more frequently or less frequently than its current trajectory.
There are any number of reasonable reasons why a flashcard’s memory model may be miscalibrated. The user may have recently learned several confuser facts that interfere with another flashcard, or the opposite, the user may have obtained an insight that crystallizes several flashcards. The user may add flashcards that they already know quite well. The user may have not studied for a long time and needs Ebisu to rescale its halflife.
I have found that anything that quiz apps can do to remove reasons for users to abandon studying is a good thing.
We can handle such explicit feedback quite readily with the GB1 time-traveling framework developed above. Recall that each flashcard has its own Ebisu model \((α, β, t)\) which specify that the probability of recall \(t\) time units after studying follows a \(Beta(α, β)\) probability distribution.
Then, we can accept a number from the user \(u > 0\) that we interpret to mean “rescale this model’s halflife by \(u\)”. This can be less than 1, meaning “shorten this halflife, it’s too long”, or greater than 1 meaning the opposite.
To achieve this command, we
- find the time \(h\) such that the probability of recall is exactly 0.5: \(h\) for “halflife”. This can be done via a one-dimensional search.
- We time-travel the \(Beta(α, β)\) distribution (which is valid at \(t\)) through Ebbinghaus’ exponential forgetting function to this halflife and obtain the GB1 distribution on probabilty recall there.
- We moment-match that GB1 distribution to a Beta random variable to obtain a new model that’s perfectly balanced: \((α_h, α_h, h)\).
- Then we simply scale the halflife with with \(u\), yielding an updated and halflife-rescaled model, \((α_h, α_h, u \cdot h)\).
The mean of the GB1 distribution on probability recall will be 0.5 by construction at the halflife \(h\): letting \(δ = \frac{h}{t}\), \[ m_1 = E[p_t^δ] = \frac{B(α+δ, β)}{B(α,β)} = \frac{1}{2}. \] The second non-central moment of GB1 distributions is also straightforward: \[ m_2 = E\left[(p_t^δ) ^ 2\right] = \frac{B(α+2δ, β)}{B(α,β)}. \] As we’ve done before, with these two moments, we can find the closest Beta random variable: letting \(μ = 0.5\) and \(σ^2 = m_2 - 0.5^2\), the recall probability at the halflife, \(h\), time units after last review is approximately \(Beta(α_h, α_h)\) where \[α_h = μ (μ(1-μ)/σ^2 - 1) = \frac{1}{8 m_2 - 2} - \frac{1}{2}.\]
All that remains is to mindlessly follow the user’s instructions and scale the halflife by \(u\).
In this way, we can rescale an Ebisu model \((α, β, t)\) to \((α_h, α_h, u \cdot h)\).
In all of the analysis above, we’ve started with a Beta prior on recall probability at some time \(t\), updated that prior with information about quizzes at time \(t_2\), only to collapse the resulting posterior back into a Beta random variable representing recall at time \(t'\). We do this so that the update step outputs the same model format as its input. However, it’s interesting to avoid approximating the posterior, and see what the exact posterior is after a series of quizzes.
As alluded to above, in certain cases, the posterior can be surprisingly simple when \(t=t'\), i.e., \(δ ε = 1\). To begin with, let’s also restrict ourselves to \(n=1\), a single quiz per review, but we will see how that can be readily relaxed for the full binomial case.
After one binary quiz \(x_1\) at time \(t_1 = δ_1 t\), the posterior is \[ P(p; p_t | x_1) ∝ \begin{cases} p^{α + δ_1 - 1} (1-p)^{β - 1}, & \text{if}\ x_1=1 \\ p^{α - 1} (1-p)^{β - 1} (1 - p^{δ_1}), & \text{if}\ x_1=0. \end{cases} \] That is, for the successful quiz case, the posterior is just \(Beta(α + δ_1, β)\), and for the unsuccessful case, the posterior is a mixture of two Beta random variables:
- \(Beta(α, β)\) with weight \(\frac{B(α, β)}{B(α, β) - B(α+δ_1, β)}\) and
- \(Beta(α + δ_1, β)\) with weight \(\frac{-B(α+δ_1, β)}{B(α, β) - B(α+δ_1, β)}\).
(We can obtain these weights by normalizing the full posterior (the weight denominators) and each term after expanding \(1-p^δ_1\).)
Usually we think of mixtures as having positive weights but this is not a hard requirement (for example, Müller et al. rely on some negative mixture weights). Weights do have to sum to 1, which is the case for us here.
For one failed quiz, our Beta prior becomes a mixture of two Beta random variables in the posterior. This should suggest that, while another successful quiz might result in a posterior that remains a mixture of two Betas, another failure would result in a mixture of four Betas. That is indeed the case: if we treat the posterior above \(P(p; p_t | x_1=0)\) as the prior and update it after another quiz after \(t_2=δ_2 t\) time units, the doubly-updated posterior is: \[ P(p; p_t | x_1=0, x_2) ∝ \begin{cases} p^{α + δ_2 - 1} (1-p)^{β - 1} (1 - p^{δ_1}), & \text{if}\ x_2=1 \\ p^{α - 1} (1-p)^{β - 1} (1 - p^{δ_1}) (1-p^{δ_2}), & \text{if}\ x_2=0. \end{cases} \] With one failed and one successful quiz, the full analytical posterior of recall probability \(t\) time units after last recall remains a mixture of two Beta random variables. Meanwhile, the posterior with two failed quizzes has expanded into a mixture of four Betas, which can be seen by expanding \((1 - p^{δ_1}) (1-p^{δ-2})\).
We can show (quite easily with Sympy) that after \(M\) single-quiz reviews that each have a quiz result \(x_m\) at a time \(t_m=δ_m t\), the full posterior is \[ P(p; p_t | x_1, x_2, …, x_M) ∝ p^{α - 1} (1-p)^{β - 1} \prod_{m=1}^M r_m p^{δ_m} + s_m, \] and since
- \(r_m=1\) and \(s_m=0\) when \(x_m=1\) (successful quiz) and
- \(r_m=-1\) and \(s_m=1\) when \(x_m=0\) (failed quiz),
this can be rewritten as \[ P(p; p_t | x_1, x_2, …, x_M) ∝ p^{α + \left( \sum_{m=1}^M I(x_m) \delta_m \right) - 1} (1-p)^{β - 1} \prod_{m=1}^M I'(x_m) (1-p^{δ_m}), \] where \(I(x)\) is the indicator function that evaluates to 1 when its argument is 1 and 0 otherwise; and its negation \(I'(x)\) evaluates to 0 when its argument is 1 and vice versa. Each successful quiz piles itself into the term on the left, leaving the updated posterior with the same number of mixture components as before. Meanwhile, each failed quiz adds a new term to the right, doubling the number of mixture components.
One way this is useful is, we can use this to double-check our binomial posterior: if \(n_1>1\), i.e., more than one quiz in the first review, that is equivalent to \(M=n_1\) with \(δ_1, δ_2, …, δ_{n_1}\) equal to the same value \(δ\). Thus, \[ P(p; p_t | k_1, n_1) ∝ p^{α + k \delta - 1} (1-p)^{β - 1} (1 - p^{δ})^{n-k}, \] which is what we saw above.
But this is also useful because now we know that that for true quizzes, we could have exact (no approximation needed) posteriors by fixing \(δ ε = 1\). For failures, meanwhile, because the posterior becomes a mixture, no single Beta can capture it perfectly, but the approximation will vary in quality depending on \(ε\).
It also opens up the possibility for re-approximating the posterior after some quizzes have happened: we could evaluate the moments of the full posterior after several quizzes (successes and failures) and find the best Beta fit, which may well be a better approximation than the series of serially-computed Beta fits after each quiz. We leave this as future work. The source code of Ebisu, which is given in the next section, will by default pick \(ε\) such that the posterior is balanced at its halflife, i.e., the probability of recall after \(t'\) time units is 0.5.
Sympy actually makes this quite easy to re-derive, which is a relief because I can never hang on to papers and it’s tiring to resurrect derivations. The script below has a function to update a symbolic prior through the quiz update and time-travel, so when you run it, it will print out the final posterior after a series of pass/fail quizzes. (It does ignore normalizing constants.) Either run this as a file on your computer or copy-paste this into Sympy Live.
from sympy import symbols, simplify p, a, b, d, e = symbols('p α β δ ε', positive=True, real=True) r, s = symbols('r s', real=True) timetravel = lambda expr, d: expr.subs(p, p**(1 / d)) * (p**(1 / d - 1)) subWithSimp = lambda expr, tiny: expr.subs(tiny, simplify(tiny)) resultToCD = {True: {r: 1, s: 0}, False: {r: -1, s: 1}} def prior_tToPosterior_t(prior, d, e, result=None, back_to_t=True): """Move the prior through a result update and time travel to get a posterior. `prior`, `d`, and `e` can/should be Sympy expressions. Let `result=None` if you want the posterior to keep `r` and `s` terms. If `result=True` or `False`, the expressions will simplify. `back_to_t=True` will replace ε with 1/δ so the posterior applies to recall at the same time as `prior`. If `back_to_t=False`, leave it as ε. """ prior_d = simplify(timetravel(prior, d)) likelihood = r * p + s posterior_d = prior_d * likelihood posterior_e = timetravel(posterior_d, e) # replace r & s if result was given subbed = resultToCD[result] if result in resultToCD else {} pf = simplify(posterior_e.subs(subbed)) # at the same time as quiz # move the pass/fail posterior from t_2 (quiz) to t' (t if back_to_t) pf_t = pf.subs(e, 1 / d if back_to_t else e) pf_t = subWithSimp(pf_t, d * (1 - 1 / d) - d) pf_t = subWithSimp(pf_t, d * (1 - e) - d) return pf_t dn = lambda n: symbols('δ_' + str(n), positive=True, real=True) en = lambda n: symbols('ε_' + str(n), positive=True, real=True) def quizSeries(prior, quizzes): "Start with prior and serially update with quiz results" for n, q in enumerate(quizzes): prior = simplify(prior_tToPosterior_t(prior, dn(n + 1), en(n + 1), result=q)) return prior prior_t = p**(a - 1) * (1 - p)**(b - 1) final = quizSeries(prior_t, [False, False, False, True]) final
In keeping with the literate programming theme of this document, I include the source code interleaved with commentary.
Python Ebisu contains a sub-module called ebisu.alternate which contains a number of alternative implementations of predictRecall and updateRecall. The __init__ file sets up this module hierarchy.
# export ebisu/__init__.py #
from .ebisu import *
from . import alternateLet’s present our Python implementation of the core Ebisu functions, predictRecall and updateRecall, and a couple of other related functions that live in the main ebisu module. All these functions consume a model encoding a Beta prior on recall probabilities at time \(t\), consisting of a 3-tuple containing \((α, β, t)\). I could have gone all object-oriented here but I chose to leave all these functions as stand-alone functions that consume and transform this 3-tuple because (1) I’m not an OOP devotee, and (2) I wanted to maximize the transparency of of this implementation so it can readily be ported to non-OOP, non-Pythonic languages.
Important Note how none of these functions deal with timestamps. All time is captured in “time since last review”, and your external application has to assign units and store timestamps (as illustrated in the Ebisu Jupyter Notebook). This is a deliberate choice! Ebisu wants to know as little about your facts as possible.
In the math section above we derived the mean recall probability at time \(t_2 = t · δ\) given a model \(α, β, t\): \(E[p_t^δ] = B(α+δ, β)/B(α,β)\), which is readily computed using Scipy’s log-beta, avoiding overflowing and precision-loss in predictRecall (🍏 below).
As a computational speedup, we can skip the final exp that converts the probability from the log-domain to the linear domain as long as we don’t need an actual probability (i.e., a number between 0 and 1). The output of the function for different models can be directly compared to each other and sorted to rank the risk of forgetting cards. Taking advantage of this optimization can, for one example, reduce the runtime from 5.69 µs (± 158 ns) to 4.01 µs (± 215 ns), a 1.4× speedup.
Another computational speedup is that we can cache calls to \(B(α,β)\), which don’t change when the function is called for same quiz repeatedly, as might happen if a quiz app repeatedly asks for the latest recall probability for its flashcards. When the cache is hit, the number of calls to betaln drops from two to one. (Python 3.2 got the nice functools.lru_cache decorator but we forego its use for backwards-compatibility with Python 2.)
# export ebisu/ebisu.py #
from scipy.special import betaln, beta as betafn, logsumexp
import numpy as np
def predictRecall(prior, tnow, exact=False):
"""Expected recall probability now, given a prior distribution on it. 🍏
`prior` is a tuple representing the prior distribution on recall probability
after a specific unit of time has elapsed since this fact's last review.
Specifically, it's a 3-tuple, `(alpha, beta, t)` where `alpha` and `beta`
parameterize a Beta distribution that is the prior on recall probability at
time `t`.
`tnow` is the *actual* time elapsed since this fact's most recent review.
Optional keyword parameter `exact` makes the return value a probability,
specifically, the expected recall probability `tnow` after the last review: a
number between 0 and 1. If `exact` is false (the default), some calculations
are skipped and the return value won't be a probability, but can still be
compared against other values returned by this function. That is, if
> predictRecall(prior1, tnow1, exact=True) < predictRecall(prior2, tnow2, exact=True)
then it is guaranteed that
> predictRecall(prior1, tnow1, exact=False) < predictRecall(prior2, tnow2, exact=False)
The default is set to false for computational efficiency.
See README for derivation.
"""
from numpy import exp
a, b, t = prior
dt = tnow / t
ret = betaln(a + dt, b) - _cachedBetaln(a, b)
return exp(ret) if exact else ret
_BETALNCACHE = {}
def _cachedBetaln(a, b):
"Caches `betaln(a, b)` calls in the `_BETALNCACHE` dictionary."
if (a, b) in _BETALNCACHE:
return _BETALNCACHE[(a, b)]
x = betaln(a, b)
_BETALNCACHE[(a, b)] = x
return xNext is the implementation of updateRecall (🍌 below), which accepts
- a
model(as above, represents the Beta prior on recall probability at one specific time since the fact’s last review), successes: the number of times the student successfully exercised this memory (possibly float for a fuzzy soft-binary quiz), out oftotaltrials (should be 1 ifsuccessesis a float), andtnow, the actual time since last quiz that this quiz was administered,- as well as a few optional arguments that power-users may find useful:
rebalance=Trueby default,tback=Noneby default, andq0=Noneby default;
and returns a new model, a 3-tuple \(α_2, β_2, t_2\), representing an updated Beta prior on recall probability over some new time horizon \(t_2\). By default, since rebalance=True, we will choose the new time horizon such that the posterior on recall probability at that time horizon is 0.5, i.e., the new time horizon is the new model’s halflife. Because of how Beta random variables work, this implies that \(α_2 = β_2\), and the new recall probability’s probability density is balanced around 0.5. This calculation can’t seem to be done analytically, so we do a one-dimensional search to find the appropriate \(t_2\). We discuss this search for the halflife below when we come to modelToPercentileDecay.
(You may choose to skip this rebalancing by passing rebalance=False. You may want to provide a different time horizon that the new model is calibrated to: pass in a specific tback then. Or you may choose to leave tback=None, in which case the function will return the new model at the same time horizon as the old model. (Recall from the [appendix])(#appendix-exact-ebisu-posteriors) that this behavior, with tback = t, will result in exact zero-approximation updates for flashcards with all successful quizzes.))
Quiz apps that only have integer quiz results don’t have to worry about the final argument q0, which only applies to quiz apps that use total == 1 and floating 0 <= successes <= 1. q0 as described above is the probability that a quiz was “really” a failure but was “scrambled” and resulted in a success—that is, the probability that a student had really forgotten this fact but still got the quiz right (and you can imagine any number of reasons for this). By default, we choose q0 such that the new model scales smoothly between the hard-fail successes = 0.0 case and the full-pass successes = 1.0 case, but you may choose to experiment with different values for q0 because you don’t like this idea that a quiz success can happen when the memory was actually gone.
I’ve chosen to break up the Bernoulli (binary and soft-binary) and the binomial cases into two separate functions. The main updateRecall (🍌) handles the binomial case, with total > 1. If n == 1, it will call a helper function _updateRecallSingle (🍅 below) that implements the (noisy-)binary update. I feel this is more readable, since computing the moments for the binomial case is more involved than the fuzzy soft-binary case.
The function uses logsumexp, which seeks to mitigate loss of precision when subtract in the log-domain. A helper function finds the Beta distribution that best matches a given mean and variance, _meanVarToBeta. Another helper function, binomln, computes the logarithm of the binomial expansion, which Scipy does not provide.
# export ebisu/ebisu.py #
def binomln(n, k):
"Log of scipy.special.binom calculated entirely in the log domain"
return -betaln(1 + n - k, 1 + k) - np.log(n + 1)
def updateRecall(prior, successes, total, tnow, rebalance=True, tback=None, q0=None):
"""Update a prior on recall probability with a quiz result and time. 🍌
`prior` is same as in `ebisu.predictRecall`'s arguments: an object
representing a prior distribution on recall probability at some specific time
after a fact's most recent review.
`successes` is the number of times the user *successfully* exercised this
memory during this review session, out of `n` attempts. Therefore, `0 <=
successes <= total` and `1 <= total`.
If the user was shown this flashcard only once during this review session,
then `total=1`. If the quiz was a success, then `successes=1`, else
`successes=0`. (See below for fuzzy quizzes.)
If the user was shown this flashcard *multiple* times during the review
session (e.g., Duolingo-style), then `total` can be greater than 1.
If `total` is 1, `successes` can be a float between 0 and 1 inclusive. This
implies that while there was some "real" quiz result, we only observed a
scrambled version of it, which is `successes > 0.5`. A "real" successful quiz
has a `max(successes, 1 - successes)` chance of being scrambled such that we
observe a failed quiz `successes > 0.5`. E.g., `successes` of 0.9 *and* 0.1
imply there was a 10% chance a "real" successful quiz could result in a failed
quiz.
This noisy quiz model also allows you to specify the related probability that
a "real" quiz failure could be scrambled into the successful quiz you observed.
Consider "Oh no, if you'd asked me that yesterday, I would have forgotten it."
By default, this probability is `1 - max(successes, 1 - successes)` but doesn't
need to be that value. Provide `q0` to set this explicitly. See the full Ebisu
mathematical analysis for details on this model and why this is called "q0".
`tnow` is the time elapsed between this fact's last review.
Returns a new object (like `prior`) describing the posterior distribution of
recall probability at `tback` time after review.
If `rebalance` is True, the new object represents the updated recall
probability at *the halflife*, i,e., `tback` such that the expected
recall probability is is 0.5. This is the default behavior.
Performance-sensitive users might consider disabling rebalancing. In that
case, they may pass in the `tback` that the returned model should correspond
to. If none is provided, the returned model represets recall at the same time
as the input model.
N.B. This function is tested for numerical stability for small `total < 5`. It
may be unstable for much larger `total`.
N.B.2. This function may throw an assertion error upon numerical instability.
This can happen if the algorithm is *extremely* surprised by a result; for
example, if `successes=0` and `total=5` (complete failure) when `tnow` is very
small compared to the halflife encoded in `prior`. Calling functions are asked
to call this inside a try-except block and to handle any possible
`AssertionError`s in a manner consistent with user expectations, for example,
by faking a more reasonable `tnow`. Please open an issue if you encounter such
exceptions for cases that you think are reasonable.
"""
assert (0 <= successes and successes <= total and 1 <= total)
if total == 1:
return _updateRecallSingle(prior, successes, tnow, rebalance=rebalance, tback=tback, q0=q0)
(alpha, beta, t) = prior
dt = tnow / t
failures = total - successes
binomlns = [binomln(failures, i) for i in range(failures + 1)]
def unnormalizedLogMoment(m, et):
return logsumexp([
binomlns[i] + betaln(alpha + dt * (successes + i) + m * dt * et, beta)
for i in range(failures + 1)
],
b=[(-1)**i for i in range(failures + 1)])
logDenominator = unnormalizedLogMoment(0, et=0) # et doesn't matter for 0th moment
message = dict(
prior=prior, successes=successes, total=total, tnow=tnow, rebalance=rebalance, tback=tback)
if rebalance:
from scipy.optimize import root_scalar
target = np.log(0.5)
rootfn = lambda et: (unnormalizedLogMoment(1, et) - logDenominator) - target
sol = root_scalar(rootfn, bracket=_findBracket(rootfn, 1 / dt))
et = sol.root
tback = et * tnow
if tback:
et = tback / tnow
else:
tback = t
et = tback / tnow
logMean = unnormalizedLogMoment(1, et) - logDenominator
mean = np.exp(logMean)
m2 = np.exp(unnormalizedLogMoment(2, et) - logDenominator)
assert mean > 0, message
assert m2 > 0, message
meanSq = np.exp(2 * logMean)
var = m2 - meanSq
assert var > 0, message
newAlpha, newBeta = _meanVarToBeta(mean, var)
return (newAlpha, newBeta, tback)
def _updateRecallSingle(prior, result, tnow, rebalance=True, tback=None, q0=None):
(alpha, beta, t) = prior
z = result > 0.5
q1 = result if z else 1 - result # alternatively, max(result, 1-result)
if q0 is None:
q0 = 1 - q1
dt = tnow / t
if z == False:
c, d = (q0 - q1, 1 - q0)
else:
c, d = (q1 - q0, q0)
den = c * betafn(alpha + dt, beta) + d * (betafn(alpha, beta) if d else 0)
def moment(N, et):
num = c * betafn(alpha + dt + N * dt * et, beta)
if d != 0:
num += d * betafn(alpha + N * dt * et, beta)
return num / den
if rebalance:
from scipy.optimize import root_scalar
rootfn = lambda et: moment(1, et) - 0.5
sol = root_scalar(rootfn, bracket=_findBracket(rootfn, 1 / dt))
et = sol.root
tback = et * tnow
elif tback:
et = tback / tnow
else:
tback = t
et = tback / tnow
mean = moment(1, et) # could be just a bit away from 0.5 after rebal, so reevaluate
secondMoment = moment(2, et)
var = secondMoment - mean * mean
newAlpha, newBeta = _meanVarToBeta(mean, var)
assert newAlpha > 0
assert newBeta > 0
return (newAlpha, newBeta, tback)
def _meanVarToBeta(mean, var):
"""Fit a Beta distribution to a mean and variance."""
# [betaFit] https://en.wikipedia.org/w/index.php?title=Beta_distribution&oldid=774237683#Two_unknown_parameters
tmp = mean * (1 - mean) / var - 1
alpha = mean * tmp
beta = (1 - mean) * tmp
return alpha, betaFinally we have some helper functions in the main ebisu namespace.
It can be very useful to predict when a given memory model expects recall to decay to an arbitrary percentile, not just 50% (i.e., half-life). Besides feedback to users, a quiz app might store the time when each quiz’s recall probability reaches 50%, 5%, 0.05%, …, as a computationally-efficient approximation to the exact recall probability. modelToPercentileDecay (🏀 below) takes a model and optionally a percentile keyword (a number between 0 and 1).
modelToPercentileDecay and both update functions above use Scipy’s root_scalar, which needs to be given a bracket to search in. _findBracket is a helper function that is used in all three functions, but it’s a general purpose function, designed by Robert Kern, to whom I’m most grateful.
As described in the section above on rescaling a model explicitly, sometimes Ebisu just isn’t working and a user might want you to outright expand or reduce the halflife of a model: rescaleHalflife does this. It simply takes a model and some number greater than zero, then finds the halflife of the model to rebalance the model, so its \(α=β\), using its first two moments. It then returns that model with the original halflife scaled by the number: if the user wants to see this flashcard less frequently, this should be greater than 1. If the user wants to see it more frequently, this should be less than one.
The least important function from a usage point of view is also the most important function for someone getting started with Ebisu: I call it defaultModel (🍗 below) and it simply creates a “model” object (a 3-tuple) out of the arguments it’s given. It’s included in the ebisu namespace to help developers who totally lack confidence in picking parameters: the only information it absolutely needs is an expected half-life, e.g., four hours or twenty-four hours or however long you expect a newly-learned fact takes to decay to 50% recall.
# export ebisu/ebisu.py #
def modelToPercentileDecay(model, percentile=0.5):
"""When will memory decay to a given percentile? 🏀
Given a memory `model` of the kind consumed by `predictRecall`,
etc., and optionally a `percentile` (defaults to 0.5, the
half-life), find the time it takes for memory to decay to
`percentile`.
"""
# Use a root-finding routine in log-delta space to find the delta that
# will cause the GB1 distribution to have a mean of the requested quantile.
# Because we are using well-behaved normalized deltas instead of times, and
# owing to the monotonicity of the expectation with respect to delta, we can
# quickly scan for a rough estimate of the scale of delta, then do a finishing
# optimization to get the right value.
assert (percentile > 0 and percentile < 1)
from scipy.special import betaln
from scipy.optimize import root_scalar
alpha, beta, t0 = model
logBab = betaln(alpha, beta)
logPercentile = np.log(percentile)
def f(delta):
logMean = betaln(alpha + delta, beta) - logBab
return logMean - logPercentile
b = _findBracket(f, init=1., growfactor=2.)
sol = root_scalar(f, bracket=b)
# root_scalar is supposed to take initial guess x0, but it doesn't seem
# to speed up convergence at all? This is frustrating because for balanced
# models the solution is 1.0 which we could initialize...
t1 = sol.root * t0
return t1
def rescaleHalflife(prior, scale=1.):
"""Given any model, return a new model with the original's halflife scaled.
Use this function to adjust the halflife of a model.
Perhaps you want to see this flashcard far less, because you *really* know it.
`newModel = rescaleHalflife(model, 5)` to shift its memory model out to five
times the old halflife.
Or if there's a flashcard that suddenly you want to review more frequently,
perhaps because you've recently learned a confuser flashcard that interferes
with your memory of the first, `newModel = rescaleHalflife(model, 0.1)` will
reduce its halflife by a factor of one-tenth.
Useful tip: the returned model will have matching α = β, where `alpha, beta,
newHalflife = newModel`. This happens because we first find the old model's
halflife, then we time-shift its probability density to that halflife. The
halflife is the time when recall probability is 0.5, which implies α = β.
That is the distribution this function returns, except at the *scaled*
halflife.
"""
(alpha, beta, t) = prior
oldHalflife = modelToPercentileDecay(prior)
dt = oldHalflife / t
logDenominator = betaln(alpha, beta)
logm2 = betaln(alpha + 2 * dt, beta) - logDenominator
m2 = np.exp(logm2)
newAlphaBeta = 1 / (8 * m2 - 2) - 0.5
assert newAlphaBeta > 0
return (newAlphaBeta, newAlphaBeta, oldHalflife * scale)
def defaultModel(t, alpha=3.0, beta=None):
"""Convert recall probability prior's raw parameters into a model object. 🍗
`t` is your guess as to the half-life of any given fact, in units that you
must be consistent with throughout your use of Ebisu.
`alpha` and `beta` are the parameters of the Beta distribution that describe
your beliefs about the recall probability of a fact `t` time units after that
fact has been studied/reviewed/quizzed. If they are the same, `t` is a true
half-life, and this is a recommended way to create a default model for all
newly-learned facts. If `beta` is omitted, it is taken to be the same as
`alpha`.
"""
return (alpha, beta or alpha, t)
def _findBracket(f, init=1., growfactor=2.):
"""
Roughly bracket monotonic `f` defined for positive numbers.
Returns `[l, h]` such that `l < h` and `f(h) < 0 < f(l)`.
Ready to be passed into `scipy.optimize.root_scalar`, etc.
Starts the bracket at `[init / growfactor, init * growfactor]`
and then geometrically (exponentially) grows and shrinks the
bracket by `growthfactor` and `1 / growthfactor` respectively.
For misbehaved functions, these can help you avoid numerical
instability. For well-behaved functions, the defaults may be
too conservative.
"""
factorhigh = growfactor
factorlow = 1 / factorhigh
blow = factorlow * init
bhigh = factorhigh * init
flow = f(blow)
fhigh = f(bhigh)
while flow > 0 and fhigh > 0:
# Move the bracket up.
blow = bhigh
flow = fhigh
bhigh *= factorhigh
fhigh = f(bhigh)
while flow < 0 and fhigh < 0:
# Move the bracket down.
bhigh = blow
fhigh = flow
blow *= factorlow
flow = f(blow)
assert flow > 0 and fhigh < 0
return [blow, bhigh]To be at feature parity with this reference implementation of Ebisu, a port should offer all of the above functions, but only the first two are essential—the rest are merely useful:
predictRecall, aided by a private helper function_cachedBetaln—core,updateRecall, aided by private helper functions_updateRecallSingleand_meanVarToBeta—core,modelToPercentileDecay—optional,rescaleHalflife—optional, anddefaultModel—optional.
The functions in the following section are either for illustrative or debugging purposes.
I wrote a number of other functions that help provide insight or help debug the above functions in the main ebisu workspace but are not necessary for an actual implementation. These are in the ebisu.alternate submodule and not nearly as much time has been spent on polish or optimization as the above core functions. However they are very helpful in unit tests.
predictRecallMode and predictRecallMedian return the mode and median of the recall probability prior rewound or fast-forwarded to the current time. That is, they return the mode/median of the random variable \(p_t^δ\) whose mean is returned by predictRecall (🍏 above). Recall that \(δ = t / t_{now}\).
Both median and mode, like the mean, have analytical expressions. The mode is a little dangerous: the distribution can blow up to infinity at 0 or 1 when \(δ\) is either much smaller or much larger than 1, in which case the analytical expression for mode may yield nonsense—I have a number of not-very-rigorous checks to attempt to detect this. The median is computed with a inverse incomplete Beta function (betaincinv), and could replace the mean as predictRecall’s return value in a future version of Ebisu.
predictRecallMonteCarlo is the simplest function but most useful. It evaluates the mean, variance, mode (via histogram), and median of \(p_t^δ\) by drawing samples from the Beta prior on \(p_t\) and raising them to the \(δ\)-power. While easy to implement and verify, Monte Carlo simulation is obviously far too computationally-burdensome for regular use.
# export ebisu/alternate.py #
from .ebisu import _meanVarToBeta
import numpy as np
def predictRecallMode(prior, tnow):
"""Mode of the immediate recall probability.
Same arguments as `ebisu.predictRecall`, see that docstring for details. A
returned value of 0 or 1 may indicate divergence.
"""
# [1] Mathematica: `Solve[ D[p**((a-t)/t) * (1-p**(1/t))**(b-1), p] == 0, p]`
alpha, beta, t = prior
dt = tnow / t
pr = lambda p: p**((alpha - dt) / dt) * (1 - p**(1 / dt))**(beta - 1)
# See [1]. The actual mode is `modeBase ** dt`, but since `modeBase` might
# be negative or otherwise invalid, check it.
modeBase = (alpha - dt) / (alpha + beta - dt - 1)
if modeBase >= 0 and modeBase <= 1:
# Still need to confirm this is not a minimum (anti-mode). Do this with a
# coarse check of other points likely to be the mode.
mode = modeBase**dt
modePr = pr(mode)
eps = 1e-3
others = [
eps, mode - eps if mode > eps else mode / 2, mode + eps if mode < 1 - eps else
(1 + mode) / 2, 1 - eps
]
otherPr = map(pr, others)
if max(otherPr) <= modePr:
return mode
# If anti-mode detected, that means one of the edges is the mode, likely
# caused by a very large or very small `dt`. Just use `dt` to guess which
# extreme it was pushed to. If `dt` == 1.0, and we get to this point, likely
# we have malformed alpha/beta (i.e., <1)
return 0.5 if dt == 1. else (0. if dt > 1 else 1.)
def predictRecallMedian(prior, tnow, percentile=0.5):
"""Median (or percentile) of the immediate recall probability.
Same arguments as `ebisu.predictRecall`, see that docstring for details.
An extra keyword argument, `percentile`, is a float between 0 and 1, and
specifies the percentile rather than 50% (median).
"""
# [1] `Integrate[p**((a-t)/t) * (1-p**(1/t))**(b-1) / t / Beta[a,b], p]`
# and see "Alternate form assuming a, b, p, and t are positive".
from scipy.special import betaincinv
alpha, beta, t = prior
dt = tnow / t
return betaincinv(alpha, beta, percentile)**dt
def predictRecallMonteCarlo(prior, tnow, N=1000 * 1000):
"""Monte Carlo simulation of the immediate recall probability.
Same arguments as `ebisu.predictRecall`, see that docstring for details. An
extra keyword argument, `N`, specifies the number of samples to draw.
This function returns a dict containing the mean, variance, median, and mode
of the current recall probability.
"""
import scipy.stats as stats
alpha, beta, t = prior
tPrior = stats.beta.rvs(alpha, beta, size=N)
tnowPrior = tPrior**(tnow / t)
freqs, bins = np.histogram(tnowPrior, 'auto')
bincenters = bins[:-1] + np.diff(bins) / 2
return dict(
mean=np.mean(tnowPrior),
median=np.median(tnowPrior),
mode=bincenters[freqs.argmax()],
var=np.var(tnowPrior))Next we have a Monte Carlo approach to updateRecall (🍌 above), the deceptively-simple updateRecallMonteCarlo. Like predictRecallMonteCarlo above, it draws samples from the Beta distribution in model and propagates them through Ebbinghaus’ forgetting curve to the time specified. To model the likelihood update from the quiz result, it assigns weights to each sample—each weight is that sample’s probability according to either the binomial or the fuzzy soft-binary likelihood. (This is equivalent to multiplying the prior with the likelihood—and we needn’t bother with the marginal because it’s just a normalizing factor which would scale all weights equally. I am grateful to mxwsn for suggesting this elegant approach.) It then applies Ebbinghaus again to move the distribution to tback. Finally, the ensemble is collapsed to a weighted mean and variance to be converted to a Beta distribution.
# export ebisu/alternate.py #
def updateRecallMonteCarlo(prior, k, n, tnow, tback=None, N=10 * 1000 * 1000, q0=None):
"""Update recall probability with quiz result via Monte Carlo simulation.
Same arguments as `ebisu.updateRecall`, see that docstring for details.
An extra keyword argument `N` specifies the number of samples to draw.
"""
# [likelihood] https://en.wikipedia.org/w/index.php?title=Binomial_distribution&oldid=1016760882#Probability_mass_function
# [weightedMean] https://en.wikipedia.org/w/index.php?title=Weighted_arithmetic_mean&oldid=770608018#Mathematical_definition
# [weightedVar] https://en.wikipedia.org/w/index.php?title=Weighted_arithmetic_mean&oldid=770608018#Weighted_sample_variance
import scipy.stats as stats
from scipy.special import binom
if tback is None:
tback = tnow
alpha, beta, t = prior
tPrior = stats.beta.rvs(alpha, beta, size=N)
tnowPrior = tPrior**(tnow / t)
if type(k) == int:
# This is the Binomial likelihood [likelihood]
weights = binom(n, k) * (tnowPrior)**k * ((1 - tnowPrior)**(n - k))
elif 0 <= k and k <= 1:
# float
q1 = max(k, 1 - k)
q0 = 1 - q1 if q0 is None else q0
z = k > 0.5 # "observed" quiz result
if z:
weights = q0 * (1 - tnowPrior) + q1 * tnowPrior
else:
weights = (1 - q0) * (1 - tnowPrior) + (1 - q1) * tnowPrior
# Now propagate this posterior to the tback
tbackPrior = tPrior**(tback / t)
# See [weightedMean]
weightedMean = np.sum(weights * tbackPrior) / np.sum(weights)
# See [weightedVar]
weightedVar = np.sum(weights * (tbackPrior - weightedMean)**2) / np.sum(weights)
newAlpha, newBeta = _meanVarToBeta(weightedMean, weightedVar)
return newAlpha, newBeta, tbackThat’s it—that’s all the code in the ebisu module!
I use the built-in unittest, and I can run all the tests from Atom via Hydrogen/Jupyter but for historic reasons I don’t want Jupyter to deal with the ebisu namespace, just functions (since most of these functions and tests existed before the module’s layout was decided). So the following is in its own fenced code block that I don’t evaluate in Atom.
In these unit tests, I compare
predictRecallagainstpredictRecallMonteCarlo, andupdateRecallagainstupdateRecallMonteCarlo, for both binomial quizzes and soft-binary quizzes.
I also want to make sure that predictRecall and updateRecall both produce sane values when extremely under- and over-reviewing (i.e., immediately after review as well as far into the future) and for a range of successes and total reviews per quiz session. And we should also exercise modelToPercentileDecay and rescaleHalflife.
For testing updateRecall, since all functions return a Beta distribution, I compare the resulting distributions in terms of Kullback–Leibler divergence (actually, the symmetric distance version), which is a nice way to measure the difference between two probability distributions. There is also a little unit test for my implementation for the KL divergence on Beta distributions.
For testing predictRecall, I compare means using relative error, \(|x-y| / |y|\).
For both sets of functions, a range of \(δ = t_{now} / t\) and both outcomes of quiz results (true and false) are tested to ensure they all produce the same answers.
Often the unit tests fails because the tolerances are a little tight, and the random number generator seed is variable, which leads to errors exceeding thresholds. I actually prefer to see these occasional test failures because it gives me confidence that the thresholds are where I want them to be (if I set the thresholds too loose, and I somehow accidentally greatly improved accuracy, I might never know). However, I realize it can be annoying for automated tests or continuous integration systems, so I am open to fixing a seed and fixing the error threshold for it.
One note: the unit tests update a global database of testpoints being tested, which can be dumped to a JSON file for comparison against other implementations.
# export ebisu/tests/test_ebisu.py
from ebisu import *
from ebisu.alternate import *
import unittest
import numpy as np
np.seterr(all='raise')
def relerr(dirt, gold):
return abs(dirt - gold) / abs(gold)
def maxrelerr(dirts, golds):
return max(map(relerr, dirts, golds))
def klDivBeta(a, b, a2, b2):
"""Kullback-Leibler divergence between two Beta distributions in nats"""
# Via http://bariskurt.com/kullback-leibler-divergence-between-two-dirichlet-and-beta-distributions/
from scipy.special import gammaln, psi
import numpy as np
left = np.array([a, b])
right = np.array([a2, b2])
return gammaln(sum(left)) - gammaln(sum(right)) - sum(gammaln(left)) + sum(
gammaln(right)) + np.dot(left - right,
psi(left) - psi(sum(left)))
def kl(v, w):
return (klDivBeta(v[0], v[1], w[0], w[1]) + klDivBeta(w[0], w[1], v[0], v[1])) / 2.
testpoints = []
class TestEbisu(unittest.TestCase):
def test_predictRecallMedian(self):
model0 = (4.0, 4.0, 1.0)
model1 = updateRecall(model0, 0, 1, 1.0)
model2 = updateRecall(model1, 1, 1, 0.01)
ts = np.linspace(0.01, 4.0, 81)
qs = (0.05, 0.25, 0.5, 0.75, 0.95)
for t in ts:
for q in qs:
self.assertGreater(predictRecallMedian(model2, t, q), 0)
def test_kl(self):
# See https://en.wikipedia.org/w/index.php?title=Beta_distribution&oldid=774237683#Quantities_of_information_.28entropy.29 for these numbers
self.assertAlmostEqual(klDivBeta(1., 1., 3., 3.), 0.598803, places=5)
self.assertAlmostEqual(klDivBeta(3., 3., 1., 1.), 0.267864, places=5)
def test_prior(self):
"test predictRecall vs predictRecallMonteCarlo"
def inner(a, b, t0):
global testpoints
for t in map(lambda dt: dt * t0, [0.1, .99, 1., 1.01, 5.5]):
mc = predictRecallMonteCarlo((a, b, t0), t, N=100 * 1000)
mean = predictRecall((a, b, t0), t, exact=True)
self.assertLess(relerr(mean, mc['mean']), 5e-2)
testpoints += [['predict', [a, b, t0], [t], dict(mean=mean)]]
inner(3.3, 4.4, 1.)
inner(34.4, 34.4, 1.)
def test_posterior(self):
"Test updateRecall via updateRecallMonteCarlo"
def inner(a, b, t0, dts, n=1):
global testpoints
for t in map(lambda dt: dt * t0, dts):
for k in range(n + 1):
msg = 'a={},b={},t0={},k={},n={},t={}'.format(a, b, t0, k, n, t)
an = updateRecall((a, b, t0), k, n, t)
mc = updateRecallMonteCarlo((a, b, t0), k, n, t, an[2], N=1_000_000 * (1 + k))
self.assertLess(kl(an, mc), 5e-3, msg=msg + ' an={}, mc={}'.format(an, mc))
testpoints += [['update', [a, b, t0], [k, n, t], dict(post=an)]]
inner(3.3, 4.4, 1., [0.1, 1., 9.5], n=5)
inner(34.4, 3.4, 1., [0.1, 1., 5.5, 50.], n=5)
def test_update_then_predict(self):
"Ensure #1 is fixed: prediction after update is monotonic"
future = np.linspace(.01, 1000, 101)
def inner(a, b, t0, dts, n=1):
for t in map(lambda dt: dt * t0, dts):
for k in range(n + 1):
msg = 'a={},b={},t0={},k={},n={},t={}'.format(a, b, t0, k, n, t)
newModel = updateRecall((a, b, t0), k, n, t)
predicted = np.vectorize(lambda tnow: predictRecall(newModel, tnow))(future)
self.assertTrue(
np.all(np.diff(predicted) < 0), msg=msg + ' predicted={}'.format(predicted))
inner(3.3, 4.4, 1., [0.1, 1., 9.5], n=5)
inner(34.4, 3.4, 1., [0.1, 1., 5.5, 50.], n=5)
def test_halflife(self):
"Exercise modelToPercentileDecay"
percentiles = np.linspace(.01, .99, 101)
def inner(a, b, t0, dts):
for t in map(lambda dt: dt * t0, dts):
msg = 'a={},b={},t0={},t={}'.format(a, b, t0, t)
ts = np.vectorize(lambda p: modelToPercentileDecay((a, b, t), p))(percentiles)
self.assertTrue(monotonicDecreasing(ts), msg=msg + ' ts={}'.format(ts))
inner(3.3, 4.4, 1., [0.1, 1., 9.5])
inner(34.4, 3.4, 1., [0.1, 1., 5.5, 50.])
# make sure all is well for balanced models where we know the halflife already
for t in np.logspace(-1, 2, 10):
for ab in np.linspace(2, 10, 5):
self.assertAlmostEqual(modelToPercentileDecay((ab, ab, t)), t)
def test_asymptotic(self):
"""Failing quizzes in far future shouldn't modify model when updating.
Passing quizzes right away shouldn't modify model when updating.
"""
def inner(a, b, n=1):
prior = (a, b, 1.0)
hl = modelToPercentileDecay(prior)
ts = np.linspace(.001, 1000, 21) * hl
passhl = np.vectorize(lambda tnow: modelToPercentileDecay(updateRecall(prior, n, n, tnow)))(
ts)
failhl = np.vectorize(lambda tnow: modelToPercentileDecay(updateRecall(prior, 0, n, tnow)))(
ts)
self.assertTrue(monotonicIncreasing(passhl))
self.assertTrue(monotonicIncreasing(failhl))
# Passing should only increase halflife
self.assertTrue(np.all(passhl >= hl * .999))
# Failing should only decrease halflife
self.assertTrue(np.all(failhl <= hl * 1.001))
for a in [2., 20, 200]:
for b in [2., 20, 200]:
inner(a, b, n=1)
def test_rescale(self):
"Test rescaleHalflife"
pre = (3., 4., 1.)
oldhl = modelToPercentileDecay(pre)
for u in [0.1, 1., 10.]:
post = rescaleHalflife(pre, u)
self.assertAlmostEqual(modelToPercentileDecay(post), oldhl * u)
# don't change halflife: in this case, predictions should be really close
post = rescaleHalflife(pre, 1.0)
for tnow in [1e-2, .1, 1., 10., 100.]:
self.assertAlmostEqual(
predictRecall(pre, tnow, exact=True), predictRecall(post, tnow, exact=True), delta=1e-3)
def test_fuzzy(self):
"Binary quizzes are heavily tested above. Now test float/fuzzy quizzes here"
fuzzies = np.linspace(0, 1, 7) # test 0 and 1 too
for tnow in np.logspace(-1, 1, 5):
for a in np.linspace(2, 20, 5):
for b in np.linspace(2, 20, 5):
prior = (a, b, 1.0)
newmodels = [updateRecall(prior, q, 1, tnow) for q in fuzzies]
for m, q in zip(newmodels, fuzzies):
# check rebalance is working
newa, newb, newt = m
self.assertAlmostEqual(newa, newb)
self.assertAlmostEqual(newt, modelToPercentileDecay(m))
# check that the analytical posterior Beta fit versus Monte Carlo
if 0 < q and q < 1:
mc = updateRecallMonteCarlo(prior, q, 1, tnow, newt, N=1_000_000)
self.assertLess(
kl(m, mc), 1e-4, msg=f'prior={prior}; tnow={tnow}; q={q}; m={m}; mc={mc}')
# also important: make sure halflife varies smoothly between q=0 and q=1
self.assertTrue(monotonicIncreasing([x for _, _, x in newmodels]))
# make sure `tback` works
prior = (3., 4., 10)
tback = 5.
post = updateRecall(prior, 1, 1, 1., rebalance=False, tback=tback)
self.assertAlmostEqual(post[2], tback)
# and default `tback` if everything is omitted is original `t`
post = updateRecall(prior, 1, 1, 1., rebalance=False)
self.assertAlmostEqual(post[2], prior[2])
def monotonicIncreasing(v):
# allow a tiny bit of negative slope
return np.all(np.diff(v) >= -1e-6)
def monotonicDecreasing(v):
# same as above, allow a tiny bit of positive slope
return np.all(np.diff(v) <= 1e-6)
if __name__ == '__main__':
unittest.TextTestRunner().run(unittest.TestLoader().loadTestsFromModule(TestEbisu()))
with open("test.json", "w") as out:
import json
out.write(json.dumps(testpoints))That if __name__ == '__main__' is for running the test suite in Atom via Hydrogen/Jupyter. I actually use nose to run the tests, e.g., python3 -m nose (which is wrapped in an npm script: if you look in package.json you’ll see that npm test will run the equivalent of node md2code.js && python3 -m "nose": this Markdown file is untangled into Python source files first, and then nose is invoked).
The code snippets here are intended to demonstrate some Ebisu functionality.
The first snippet produces the half-life plots shown above, and included below, scroll down.
import scipy.stats as stats
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
plt.rcParams['svg.fonttype'] = 'none'
t0 = 7.
ts = np.arange(1, 301.)
ps = np.linspace(0, 1., 200)
ablist = [3, 12]
plt.close('all')
plt.figure()
[
plt.plot(
ps, stats.beta.pdf(ps, ab, ab) / stats.beta.pdf(.5, ab, ab), label='α=β={}'.format(ab))
for ab in ablist
]
plt.legend(loc=2)
plt.xticks(np.linspace(0, 1, 5))
plt.title('Confidence in recall probability after one half-life')
plt.xlabel('Recall probability after one week')
plt.ylabel('Prob. of recall prob. (scaled)')
plt.savefig('figures/models.svg')
plt.savefig('figures/models.png', dpi=300)
plt.show()
plt.figure()
ax = plt.subplot(111)
plt.axhline(y=t0, linewidth=1, color='0.5')
[
plt.plot(
ts,
list(map(lambda t: modelToPercentileDecay(updateRecall((a, a, t0), xobs, t)), ts)),
marker='x' if xobs == 1 else 'o',
color='C{}'.format(aidx),
label='α=β={}, {}'.format(a, 'pass' if xobs == 1 else 'fail'))
for (aidx, a) in enumerate(ablist)
for xobs in [1, 0]
]
plt.legend(loc=0)
plt.title('New half-life (previously {:0.0f} days)'.format(t0))
plt.xlabel('Time of test (days after previous test)')
plt.ylabel('Half-life (days)')
plt.savefig('figures/halflife.svg')
plt.savefig('figures/halflife.png', dpi=300)
plt.show()This second snippet addresses a potential approximation which isn’t too accurate but might be useful in some situations. The function predictRecall (🍏 above) in exact mode evaluates the log-gamma function four times and an exp once. One may ask, why not use the half-life returned by modelToPercentileDecay and Ebbinghaus’ forgetting curve, thereby approximating the current recall probability for a fact as 2 ** (-tnow / modelToPercentileDecay(model))? While this is likely more computationally efficient (after computing the half-life up-front), it is also less precise:
ts = np.linspace(1, 41)
modelA = updateRecall((3., 3., 7.), 1, 15.)
modelB = updateRecall((12., 12., 7.), 1, 15.)
hlA = modelToPercentileDecay(modelA)
hlB = modelToPercentileDecay(modelB)
plt.figure()
[
plt.plot(ts, predictRecall(model, ts, exact=True), '.-', label='Model ' + label, color=color)
for model, color, label in [(modelA, 'C0', 'A'), (modelB, 'C1', 'B')]
]
[
plt.plot(ts, 2**(-ts / halflife), '--', label='approx ' + label, color=color)
for halflife, color, label in [(hlA, 'C0', 'A'), (hlB, 'C1', 'B')]
]
# plt.yscale('log')
plt.legend(loc=0)
plt.ylim([0, 1])
plt.xlabel('Time (days)')
plt.ylabel('Recall probability')
plt.title('Predicted forgetting curves (halflife A={:0.0f}, B={:0.0f})'.format(hlA, hlB))
plt.savefig('figures/forgetting-curve.svg')
plt.savefig('figures/forgetting-curve.png', dpi=300)
plt.show()This plot shows predictRecall’s fully analytical solution for two separate models over time as well as this approximation: model A has half-life of eleven days while model B has half-life of 7.9 days. We see that the approximation diverges a bit from the true solution.
This also indicates that placing a prior on recall probabilities and propagating that prior through time via Ebbinghaus results in a different curve than Ebbinghaus’ exponential decay curve. This surprising result can be seen as a consequence of Jensen’s inequality, which says that \(E[f(p)] ≥ f(E[p])\) when \(f\) is convex, and that the opposite is true if it is concave. In our case, \(f(p) = p^δ\), for δ = t / halflife, and Jensen requires that the accurate mean recall probability is greater than the approximation for times greater than the half-life, and less than otherwise. We see precisely this for both models, as illustrated in this plot of just their differences:
plt.figure()
ts = np.linspace(1, 14)
plt.axhline(y=0, linewidth=3, color='0.33')
plt.plot(ts, predictRecall(modelA, ts, exact=True) - 2**(-ts / hlA), label='Model A')
plt.plot(ts, predictRecall(modelB, ts, exact=True) - 2**(-ts / hlB), label='Model B')
plt.gcf().subplots_adjust(left=0.15)
plt.legend(loc=0)
plt.xlabel('Time (days)')
plt.ylabel('Difference')
plt.title('Expected recall probability minus approximation')
plt.savefig('figures/forgetting-curve-diff.svg')
plt.savefig('figures/forgetting-curve-diff.png', dpi=300)
plt.show()I think this speaks to the surprising nature of random variables and the benefits of handling them rigorously, as Ebisu seeks to do.
Below is the code to show the histograms on recall probability two days, a week, and three weeks after the last review:
def generatePis(deltaT, alpha=12.0, beta=12.0):
import scipy.stats as stats
piT = stats.beta.rvs(alpha, beta, size=50 * 1000)
piT2 = piT**deltaT
plt.hist(piT2, bins=20, label='δ={}'.format(deltaT), alpha=0.25, normed=True)
[generatePis(p) for p in [0.3, 1., 3.]]
plt.xlabel('p (recall probability)')
plt.ylabel('Probability(p)')
plt.title('Histograms of p_t^δ for different δ')
plt.legend(loc=0)
plt.savefig('figures/pidelta.svg')
plt.savefig('figures/pidelta.png', dpi=150)
plt.show()- Python
- scipy, numpy
- nose for tests
- Pandoc
- pydoc-markdown
A huge thank you to bug reporters and math experts and contributors!
Many thanks to mxwsn and commenters as well as jth for their advice and patience with my statistical incompetence.
Many thanks also to Drew Benedetti for reviewing this manuscript.
John Otander’s Modest CSS is used to style the Markdown output.