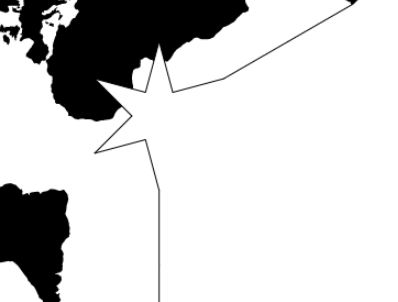
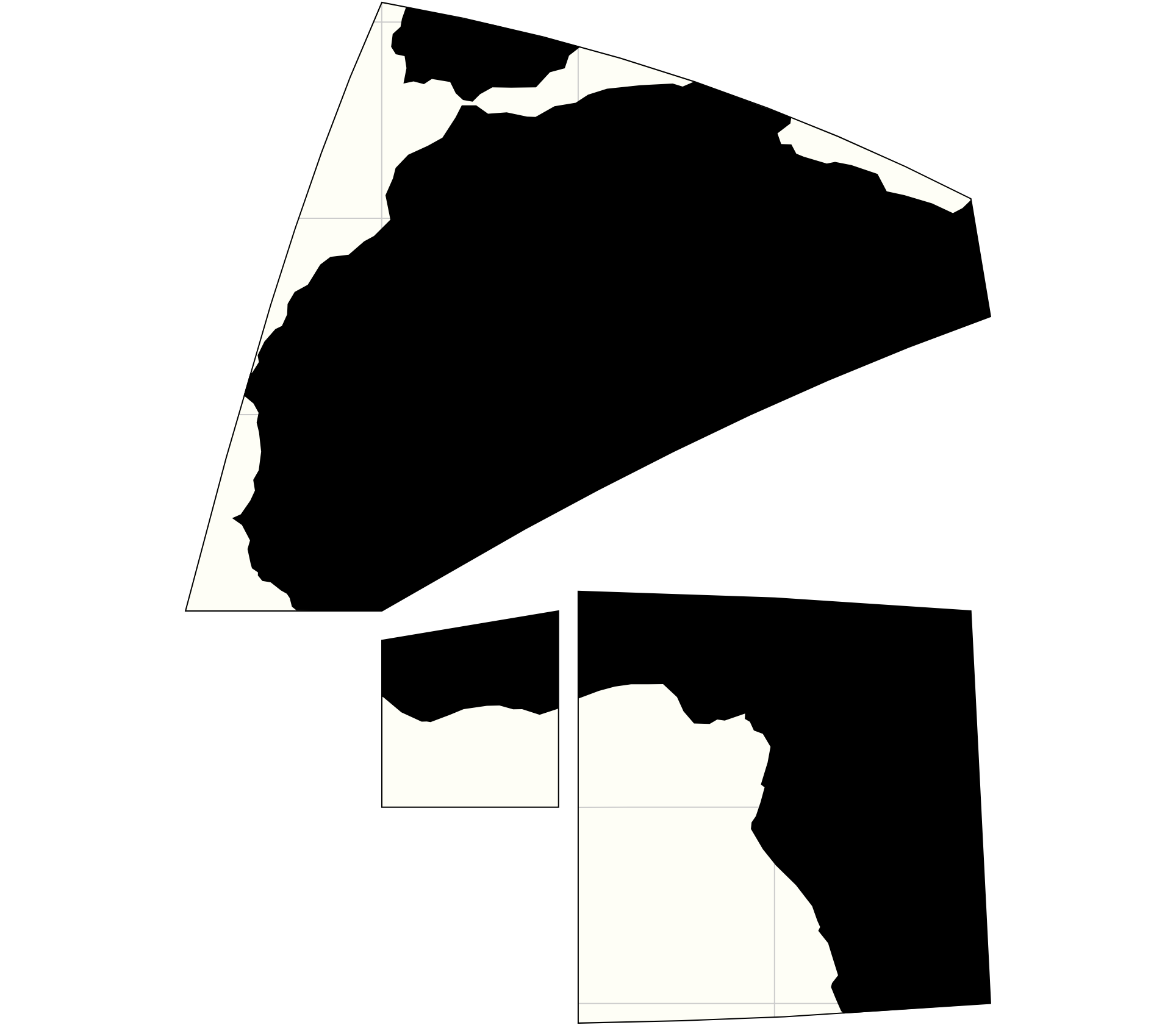
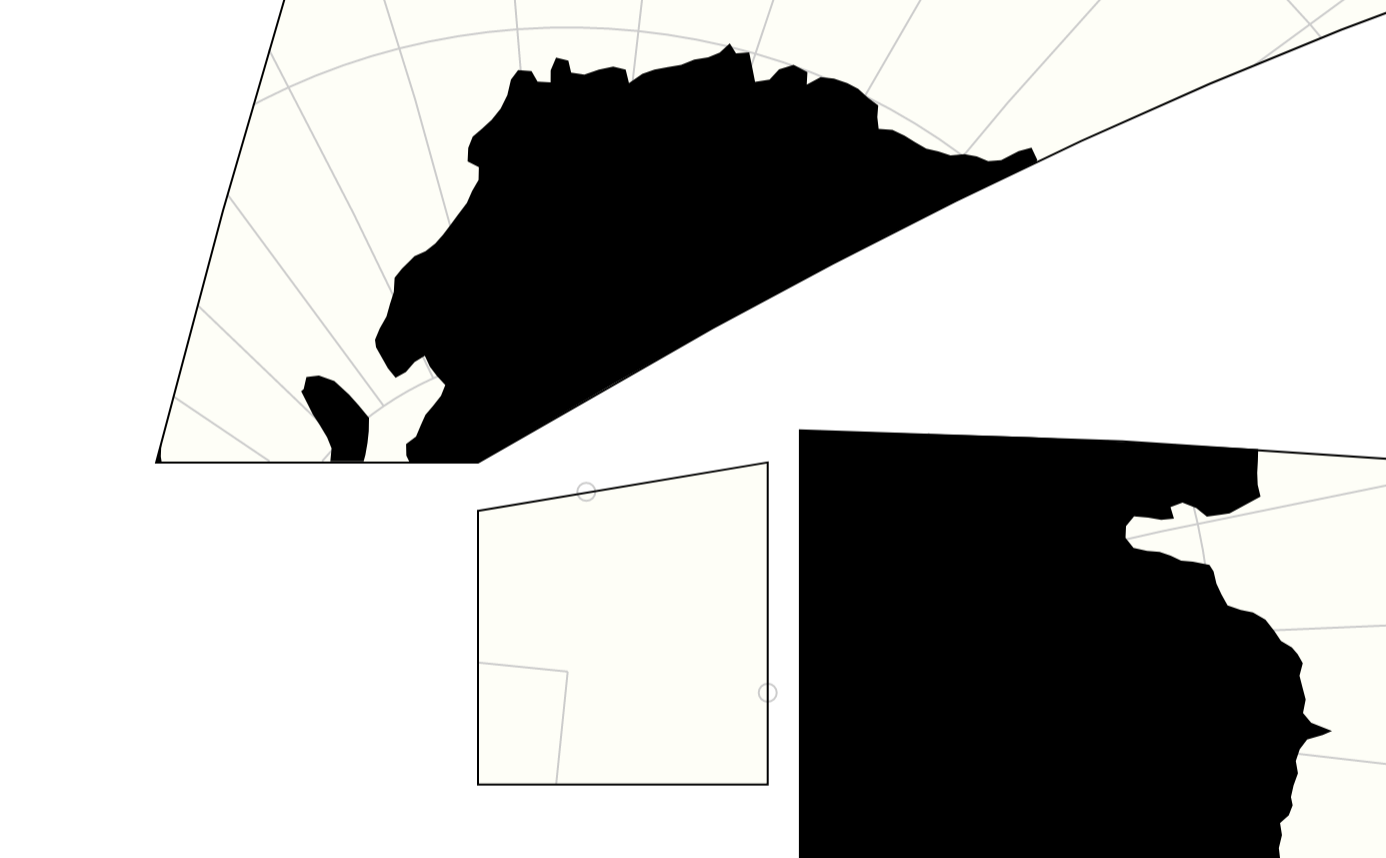
So i was trying to create a rhombic dodecahedron projection but there is something weird going on with the clipping
rhombic_f = {
var degrees = 180 / Math.PI;
var phi1 = Math.atan(Math.SQRT1_2) * degrees;
var vertices = [
[0, 90], // 0
[0, phi1], // 1
[90, phi1], // 2
[180, phi1], // 3
[-90, phi1], // 4
[45, 0], // 5
[135, 0], // 6
[-135, 0], // 7
[-45, 0], // 8
[0, -phi1], // 9
[90, -phi1], // 10
[180, -phi1], // 11
[-90, -phi1], // 12
[0, -90] // 13
];
// rhombic dodecahedron
var polyhedron = [
[0, 1, 8, 4],
[0, 2, 5, 1],
[0, 3, 6, 2],
[0, 4, 7, 3],
[1, 5, 9, 8],
[2, 6, 10, 5],
[3, 7, 11, 6],
[4, 8, 12, 7],
[8, 9, 13, 12],
[5, 10, 13, 9],
[6, 11, 13, 10],
[7, 12, 13, 11]
].map(function(face) {
return face.map(function(i) {
return vertices[i];
});
});
var polygons = {
type: "FeatureCollection",
features: polyhedron.map(function(face) {
face.push(face[0]);
return {
properties: { sitecoordinates: d3.geoCentroid({type:"MultiPoint", coordinates: face}) },
geometry: {
type: "Polygon",
coordinates: [ face ]
}
};
})
};
var parents = [
-1, // 0
0, // 1
6, // 2
2, // 3
1, // 4
9, // 5
11, // 6
3, // 7
4, // 8
8, // 9
5, // 10
10, // 11
];
//return polygons;
return d3.geoPolyhedralVoronoi()
.parents(parents)
.polygons(polygons);
};
i numbered the faces in the image below and there should be red lines around all the faces. This is a combination of the cubic and the octahedron projection.